Una proporción singular
Buscando proporciones matemáticas en los elementos decorativos de las fachadas de la Catedral de Granada no pasa desapercibido un curioso friso de triglifos y metopas. Concretamente, se observa en la fachada lateral de la nave principal que da a la Plaza de Alonso Cano. Entre los triglifos, rectángulos con tres piezas en relieve que acaban en seis gotas de forma trapezoidal llamada la régula, se sitúan las metopas, superficies cuadradas que contienen una decoración de bucráneos, osamentas de buey de cuyos cuernos cuelgan unas guirnaldas.
Continuamos analizando y observando con nuestro ojo matemático la fachada de la Catedral de Granada. Buscando proporciones matemáticas en sus elementos decorativos, no pasa desapercibido un curioso friso de triglifos y metopas. Concretamente, nos situamos en la fachada lateral de la nave principal que da a la Plaza de Alonso Cano.
Los triglifos son rectángulos con tres piezas en relieve que acaban en seis gotas de forma trapezoidal llamada la régula. Entre estos adornos se sitúan las metopas, superficies cuadradas que contienen una decoración de bucráneos, osamentas de buey de cuyos cuernos cuelgan unas guirnaldas.

Triglifos y metopas.
Como se puede observar, este friso contiene 2 metopas con sus respectivos bucráneos y sus proporciones son de √2 para los triglifos (formato vertical) y una proporción de 8:7 para las metopas (formato horizontal).
La proporción de √2 ha aparecido en diversos lugares de nuestros paseos matemáticos, pero la proporción 8:7 es algo más singular. Se construye matemáticamente sobre la base de un cuadrado con su lado dividido en 7 partes iguales y se añade una de éstas a continuación sobre el mismo lado. Se obtiene así un rectángulo como el de la siguiente figura:
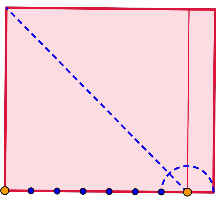
Construcción proporción 8:7.
Aunque es una proporción poco frecuente, se puede encontrar en las medidas para la construcción renacentista. Igualmente, ha sido empleada en otras tendencias y estilos arquitectónicos como las bóvedas del refectorio del monasterio cisterciense de Santa María de Huerta (siglo XIII) o en el crucero de la catedral de Sigüenza (siglo XV). También Vitruvio señala en uno de sus libros una disminución igual (de 8 a 7) para las columnas más altas.
Una proporción que, aunque poco utilizada, ayuda a mantener la concordia entre todos los elementos decorativos de la fachada de esta armónica montaña suavizando el aspecto rudo y sólido de su arquitectura.
Más sobre paseos matemáticos
El atún también 'esconde' su lado más matemático y un análisis geométrico de su cuerpo permite diferenciarlos de otros peces. En concreto, se puede saber si un pez es un atún por su cola. Así lo ha analizado en este artículo publicado en el portal web iDescubre por el director científico de Paseos Matemáticos Álvaro Martínez Sevilla. curiosidades que explican por qué este túnido juega un papel destacado en la cultura bereber.
El Instituto Español Lope de Vega de Nador ha acogido la inauguración de la exposición ‘Paseo Matemático Al-Ándalus’ de la Fundación Descubre. La muestra, que inició su andadura por territorio marroquí en Fez en 2023, está itinerando por los Institutos Españoles de Marruecos, gracias al acuerdo con el Instituto Cervantes de Fez.
La muestra podrá visitarse hasta el 14 de junio en la sala de exposiciones del Castillo.




