Un paseo y curvas catenarias

En esta nueva entrada vamos a realizar una ruta para visitar dos de los lugares más importantes de Granada, el Ayuntamiento y la Catedral, de la mano de una curva muy importante en la arquitectura: la catenaria.

Una catenaria es la curva resultante al dejar una cuerda o cadena sin peso sostenido, sujeta por sus dos extremos y sometida únicamente al efecto uniforme de la gravedad.

A lo largo de la historia, matemáticos como Da Vinci o Galileo se interesaron por dar explicación a la forma que adopta una cuerda sujeta por sus extremos, llegando incluso Galileo a afirmar que la forma de esta curva era una parábola. Por su parte, Christiaan Huygens pudo demostrar que esto no era posible, aunque lo hizo sin poder obtener la fórmula matemática que describía esta curva. En el siglo XVII, Jacob Bernoulli planteó el desafío de encontrar la ecuación que describía esta curva, el cual fue resuelto finalmente en 1961 por Gottfried Leibniz, el propio Christiaan Huygens y Johann Bernoulli.

La curva catenaria puede definirse matemáticamente con la expresión f(x) = a·cosh(x/a), donde cosh representa la función trigonométrica de coseno hiperbólico.

Si empezamos nuestro paseo catenario por el Ayuntamiento de Granada, recordamos que la escultura sobre la fachada del edificio está inspirada en el dibujo del autor tarifeño Pérez Villalta titulado “El instante preciso”. Su autor tiene una habilidad especial para el trazado a mano alzada de estas curvas y no pasa desapercibido en este dibujo, como bien puede verse en la siguiente imagen en color rojo sobre la circunferencia azul:

A continuación nos dirigimos a la Catedral de Granada, situada en la céntrica calle Gran Vía de Colón. Aquí son muchas las referencias matemáticas que podemos analizar y de las que nos ocuparemos en futuras entradas. Pero aquí vamos a observar un adorno de su fachada. Se trata de dos ángeles adornados con guirnaldas de flores con un extremo en una mano y el otro sujeto a una cuerda. Podemos suponer que este adorno describe una catenaria, si bien es cierto que es una aproximación difícil de precisar por la indefinición del trazo de borde de la cadena de guirnaldas, tal y como puede verse en la siguiente figura:

Catenarias en las guirnaldas

Por último, cerca de la Catedral, concretamente en la calle Cárcel Baja próxima a la Puerta del Perdón, nos encontramos con un elemento arquitectónico muy común en un entorno urbano: unas cadenas de gruesos pilones que describen una curva catenaria:

Catenaria en una cadena

Esta aproximación es algo más exacta, aunque con una pequeña desviación debido a que los soportes de sujeción están a distinta altura por tener cierta pendiente la calle.

Esta imagen nos sirve para proponer una interesante actividad con este paseo matemático: identificar y representar catenarias en otros lugares de interés cultural. Esta representación es fácil de llevar a cabo utilizando el software matemático Geogebra siguiendo los siguientes pasos:

1. Tomamos una fotografía y la insertamos en Geogebra. Es conveniente intentar dejar el punto más bajo de la catenaria en el origen de coordenadas para simplificar el proceso. A continuación, es necesario poner la opacidad de la imagen a un 50% y escribir en el campo de entrada tres valores diferentes: a a=1, b=1 y c=1. Así tendremos tres deslizadores que nos permitirán ajustar fácilmente la gráfica a nuestra imagen.

2. Escribimos en la entrada la ecuación de la catenaria utilizando los deslizadores de la siguiente manera:

f(x)=a*cosh((x-b)/a)+c

A continuación se pueden buscar los valores para a, b y c que permiten ajustar la representación gráfica de la función a la imagen que hemos utilizado.

Como ejemplo, vemos en la siguiente imagen una catenaria que se encuentra en la ciudad de Córdoba, frente al Palacio de la Merced, antiguo convento de la Merced Calzada y hoy sede de la Diputación Provincial de Córdoba. La siguiente imagen corresponde con una representación gráfica de la catenaria hecha con el software Geogebra:

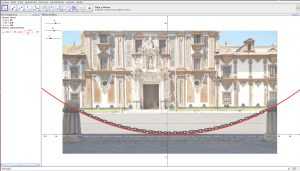
Construcción de una catenaria con Geogebra

Esperamos que este ejemplo sirva para animar a los lectores a buscar la ecuación de la catenaria que se ajusta a un elemento arquitectónico que encuentren en cualquiera de sus paseos matemáticos, de la misma forma que lo hemos hecho en nuestro paseo por Córdoba y Granada.