Frisos y simetrías en la Puerta del Perdón II
La Puerta del Perdón de la Catedral de Granada esconde peculiares simetrías que caracterizan otras ornamentas de esta fachada. En concreto, el capitel de las columnas dóricas rematado por una peana que define una curva astroide delimitada por el chaflán del propio capitel. Este elemento arquitectónico tiene un importante atractivo visual; parece que su cuidada estética consigue atraer la atención del visitante. Por este motivo, la curvatura que se observa en las figuras femeninas no es casual y ayuda a transmitir esta sensación de armonía.
En la anterior entrada nos detuvimos a observar con nuestro foco matemático sobre los elementos decorativos de la Puerta del Perdón de la Catedral de Granada. En esta ocasión vamos a continuar observando las peculiares simetrías que caracterizan otras ornamentas de esta fachada.
Concretamente, vamos a fijar nuestra atención en el capitel de las columnas dóricas rematado por una peana que define una curva astroide delimitada por el chaflán del propio capitel.
Capitel de la Puerta del Perdón.
Como se puede observar en la imagen, bajo estas esquinas destaca la presencia de dos figuras propias del imaginario de Siloé. En particular, dos figuras híbridas con torso femenino que tapan sus pechos con las manos. Estas figuras están caracterizadas con una especie de cola, la cual emerge en ambos casos de un cilindro cónico.
La disposición de estas dos figuras es perfectamente simétrica respecto al eje caracterizado con línea discontinua roja. Además, se puede observar que estas figuras están acompañadas por unas cabezas de animal, también colocadas de forma simétrica.
Sin duda, este capitel tiene un importante atractivo visual; parece que su cuidada estética consigue atraer la atención del visitante. Por este motivo, entendemos que la curvatura que se observa en las figuras femeninas no es casual y ayuda a transmitir esta sensación de armonía.
Concretamente, la curva que describe cada uno de estos cuerpos se corresponde con el brazo de una espiral áurea o espiral de Fibonacci:
Espiral áurea
Esta espiral se construye mediante rectángulos áureos agrandándose y envolviéndose sobre sí mismos. Para trazar dicha espiral basta con unir las esquinas opuestas de los cuadrados base con tramos consecutivos de arcos de circunferencia.
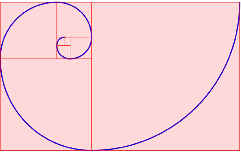
Construcción con Geogebra.
Sin perder detalle, se puede observar que el cierre de la espiral lleva directamente a lo que parece ser un tocado en el pelo de cada figura y que reproduce la continuación de la espiral.
Sin duda alguna, este capitel destaca por su belleza, singularidad y maestría compositiva.
Más sobre paseos matemáticos
La muestra podrá visitarse hasta el 19 de julio en la sede cordobesa de Casa Árabe. Se llevarán a cabo actividades complementarias el viernes 12 de abril y los sábados 4 y 11 de mayo.
El Centro de Recepción de Visitantes de Alcaudete (Jaén) ha acogido la inauguración de la exposición ‘Paseo Matemático Al-Ándalus’, un acto que ha contado con la presencia de los concejales de Educación y Turismo, Diana López y Rafael Yeguas, respectivamente, así como la directora general de Fundación Descubre, Teresa Cruz Sánchez, y el director científico del proyecto, Álvaro Martínez Sevilla.
La sede de la Organización de la Liga Árabe para la Educación, la Cultura y las Ciencias (ALECSO) acoge la muestra hasta el 15 de febrero. Esta es la primera exposición de Fundación Descubre traducida al árabe.
