Armonía geométrica en una reja de hierro: la reja de la calle Oficios 2
¿Cómo se construyen los distintos elementos del arco conopial que compone el diseño superior de la reja de la calle Oficios? En esta entrada se dan a conocer las semicircunferencias de igual radio, los arcos de medio punto y otros arcos trebolados que componen esta estructura de hierro y en la que las matemáticas juegan un papel fundamental.
En la anterior entrada de nuestro paseo matemático por Granada, hicimos una parada en el emblemático conjunto de la reja de la calle Oficios para destacar los distintos elementos matemáticos que se pueden observar en esta obra de arte matemático en hierro.
Reja de la calle Oficios
El conjunto está presidido por un arco conopial, en cuya parte interior se encajan tres semicircunferencias de igual radio, definiendo las dos inferiores dos arcos de medio punto. Estos arcos tienen inscritos otros arcos trebolados. Bajo este conjunto, una curva semielíptica ayuda a delimitar la puerta de entrada y deja reposar dos circunferencias con tetralóbulos y en cuyo interior se encuentran las iniciales Y y F.
Vamos a ver cómo sería la construcción de los distintos elementos que nos encontramos en este conjunto.
En primer lugar, trataremos el arco que delimita el conjunto en su parte superior. Se trata de un arco conopial equilátero o flamígero con 3 centros.
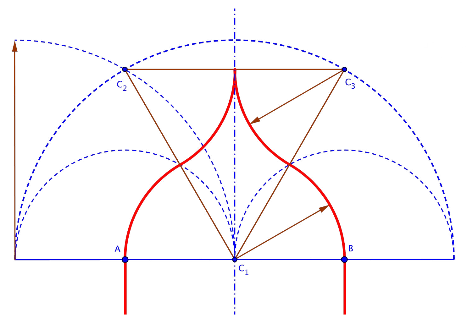
Construcción de arco conopial equilátero
Se dibuja con un triángulo equilátero abierto con vértice C1 sobre el punto medio de la línea de arranques AB. Con centro en los puntos A y B se trazan dos semicircunferencias tangentes en C1, cuyas intersecciones con el triángulo equilátero dan lugar a los puntos de unión de los 4 trozos que forman el arco: el primero y el último son convexos con centro C1 , el segundo y el tercero cóncavos y tienen el centro en los otros dos vértices del triángulo equilátero, C2 y C3.
El segundo conjunto de figuras que vamos a analizar es el de los arcos de medio punto tangentes entre sí en los puntos R, S y T. Estos arcos no comparten con el conopial la línea de arranques, pero gracias a una construcción dinámica con Geogebra es posible definir la línea de arranques de estos arcos, tal y como quedan configurados en la reja, un poco por encima de la anterior.
Este es el inicio de las dos semicircunferencias inferiores, quedando la tercera tangente a estas dos haciendo un apilamiento de Kepler y tomando como centro un punto en el eje de simetría del conjunto y con una altura determinada por el triángulo equilátero UVW. A su vez, los vértices de este triángulo definen los centros de estas tres semicircunferencias.
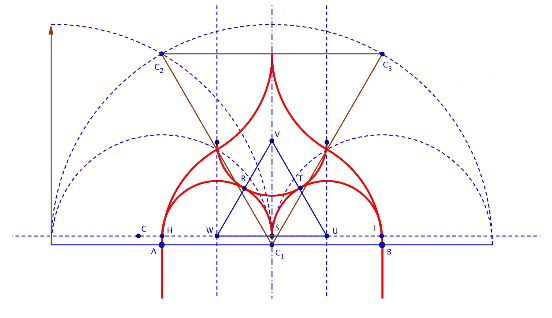
Construcción de arcos de medio punto.
Estas dos representaciones son un ejemplo de arquitectura muy características del gótico tardío y que conllevan una sencilla representación con el software Geogebra. Reproducir este tipo de elementos arquitectónicos desde una perspectiva matemática es una gran oportunidad para abordar la arquitectura de nuestro patrimonio desde una perspectiva transversal, con la construcción geométrica como eje principal.
Más sobre paseos matemáticos
Las instalaciones del antiguo Consulado francés, ubicadas en el casco antiguo de Trípoli, han acogido la inauguración de la exposición ‘Paseo Matemático al-Ándalus’ de la Fundación Descubre / Consejería de Universidad, Investigación e Innovación de la Juntade Andalucía. La muestra llega de la mano de la Embajada de España en Libia, la Agencia Española de Cooperación Internacional para el Desarrollo (AECID), el Instituto Cervantes y Old Tripoli City Administration Board.
El atún también 'esconde' su lado más matemático y un análisis geométrico de su cuerpo permite diferenciarlos de otros peces. En concreto, se puede saber si un pez es un atún por su cola. Así lo ha analizado en este artículo publicado en el portal web iDescubre por el director científico de Paseos Matemáticos Álvaro Martínez Sevilla. curiosidades que explican por qué este túnido juega un papel destacado en la cultura bereber.
El Instituto Español Lope de Vega de Nador ha acogido la inauguración de la exposición ‘Paseo Matemático Al-Ándalus’ de la Fundación Descubre. La muestra, que inició su andadura por territorio marroquí en Fez en 2023, está itinerando por los Institutos Españoles de Marruecos, gracias al acuerdo con el Instituto Cervantes de Fez.
