La Casa de los Tiros 2: las figuras en superposición

En esta nueva entrada, continuamos frente a la fachada del Museo Casa de los Tiros con el foco puesto en la presencia de las tres figuras que usamos anteriormente: el triángulo, el cuadrado y el círculo.

Superposición de tres figuras.

Si tomamos la superposición de estas tres figuras, además del círculo inscrito a partir de las consideraciones hechas de que el triángulo y el cuadrado tiene lado L y que el octógono está inscrito en el rectángulo, la construcción geométrica sería:

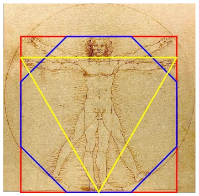
Figuras en el Hombre de Vitruvio.

Aunque a simple vista pueda parecer una construcción relativamente sencilla, no es común encontrar esta misma composición de polígonos inscritos en la historia del arte. Quizá sea debido a la dificultad estética de presentar estas tres figuras superpuestas en una armonía estética. Pero es posible encontrarla en una de las obras más conocidas del Renacimiento: el Hombre de Vitruvio, dibujo de Leonardo Da Vinci.

Esta obra presenta el canon de perfección para las proporciones del cuerpo humano, concepto sobre la figura humana que fue planteado originalmente por el arquitecto y tratadista Vitruvio. En esta obra destaca principalmente el orden matemático y la simetría del cuerpo humano como esencia del universo, representando en el ombligo el centro de gravedad.

En esta superposición de polígonos, los pies apoyan sobre los lados del octógono (representado en color azul), mientras que el triángulo en sentido invertido define la posición de los brazos extendidos en horizontal y mide la distancia desde su base al cuadrado en el que está inscrito y que separa la barbilla de la coronilla, de la cual Vitruvio afirmaba que era la octava parte de la altura de todo el cuerpo.

Para realizar la superposición de estas figuras con regla y compás, podemos fijarnos en la siguiente imagen:

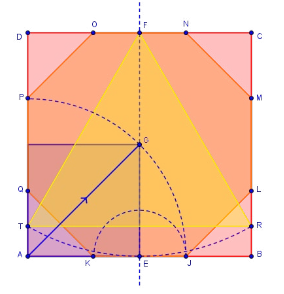
Construcción geométrica.

Esta construcción está inspirada en la representación de Arquímedes para poder medir el perímetro de una circunferencia con el objetivo de calcular el valor del número π.

Partiendo de un hexágono inscrito en una circunferencia, define sucesivamente polígonos igualmente inscritos duplicando el número de lados: 12, 24, 48 y 96 lados. Calculando el perímetro de las figuras inscritas, definió un procedimiento recursivo de rápida convergencia que le permitió obtener un valor de π=3,1410 en un polígono de 96 lados.

Pero volvamos a los polígonos presentes en la fachada del Museo Casa de Los Tiros de Granada. Para completar la observación a partir del enfoque matemático sobre estos elementos, vamos a considerar una aproximación numérica de los datos expuestos en la tabla de la anterior entrada de este blog (Figuras geométricas en la Casa de Los Tiros) sobre el perímetro y área de estas figuras, para establecer la siguiente desigualdad en relación al perímetro de estos elementos: P(t) ≤ P(o) ≤ P(c) → 3·L ≤ 3,31·L ≤ 4·L

Si atendemos igualmente al área de estas figuras, podemos establecer la siguiente desigualdad: A(t) ≤ A(o) ≤ A(c) → 0,43·L² ≤  0,82·L² ≤ L²

Así, establecemos con este enfoque matemático un argumento más para entender la disposición de las figuras y el motivo por el cual encontramos al cuadrado en el centro, en el lugar predominante: es la figura con mayor perímetro y mayor área.

Para terminar, te proponemos a ti, que estás leyendo este post, que busques elementos similares en algún edificio de tu ciudad. Te proponemos establecer una relación similar entre áreas y perímetros para poder completar esta tarea de observación matemática en nuestro patrimonio cultural.