El pentágono, una figura peculiar en la arquitectura
En la anterior entrada de nuestro blog se hizo una reconstrucción de la popular puerta del Cadí empleando el software Geogebra para estimar la altura que podía haber tenido esta emblemática estructura. Igualmente, se hizo referencia a la presencia de una escalera interior que daba acceso a las aguas del río por una puerta que todavía puede hoy verse tapiada con ladrillo. Y es aquí, en esta puerta y la escalera interior que le da acceso en lo que vamos a centrar el enfoque de nuestro paseo matemático.
En primer lugar, vemos que el dintel de la puerta está construido con dovelas que fugan hacia un punto en medio de la puerta. Igualmente, destacan la presencia de dos muescas verticales que recorren el pie del arco de arriba abajo y que podían servir para deslizar los tableros que cerraban la puerta del Cadí.

Puerta de acceso al río.
Desde el punto de vista matemático sabemos que este soporte tenía forma hexagonal, diseño que ayuda a reforzar la construcción y dar estabilidad a la estructura. Por otro lado, este trazado permitió la construcción de una doble escalera interior para acceder al nivel del agua.
¿Por qué una doble escalera? Sabemos que el agua era un bien muy preciado y necesario para usos domésticos y de riegos en la Granada zirí, de manera que este tipo de escalera garantizaba el acceso y permitía una mayor capacidad de tránsito.
Al tener que construir una doble escalera fue necesario diseñar un hexágono con los lados centrales alargados, lo cual dio lugar a dos recintos con forma de pentágono irregular. Además, dado que el muro interior es un muro de carga es necesario que sea más grueso. Esto obliga igualmente a crear un pentágono irregular en el interior con dos ángulos rectos y otros tres de 120º, aunque presentan una pequeña diferencia de estos valores.
En la siguiente imagen pueden verse estos datos numéricos para la construcción de la escalera, a partir de una imagen tomada del Archivo del Patronato de la Alhambra y el Generalife y trabajada con Geogebra:
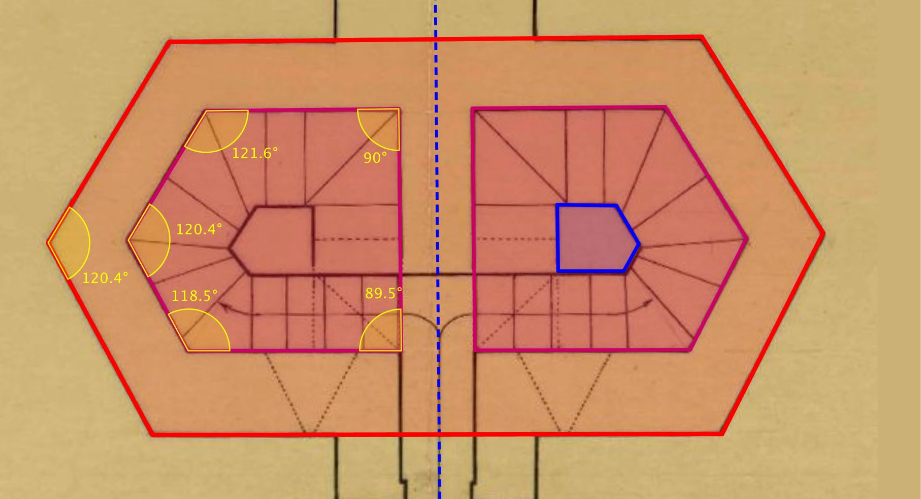
Esquema del espacio interior
La desviación en estos valores puede ser comprensible si se tiene en cuenta la inexactitud propia de una construcción de esta época en la que no se contaba con instrumentos de precisión. Si bien, partiendo de esta misma consideración, es igualmente sorprendente que la variación sea tan pequeña.
La presencia de una figura pentagonal para una construcción no es muy común, por lo que vamos a aprovechar esta singularidad para hacer referencia a otros dos lugares, fuera de la provincia de Granada, que destacan por tener forma pentagonal.
En primer lugar, nos dirigimos al pueblo de Alcalá de Júcar, en Albacete. Aquí nos encontramos con el castillo de Alcalá de Júcar. Una construcción pentagonal con forma afilada que data de origen almohade y que fue edificado entre los siglos XII y XIII.

Castillo de Alcalá de Júcar.
El otro es el castillo de Zafra en Campillo de Dueñas, Guadalajara. Es un castillo cuya torre del homenaje tiene forma pentagonal en punta de lanza. Su construcción es probablemente almohade, aunque se cree que pudo ser alzado sobre anteriores fortalezas celtibéricas y visigóticas.

Castillo de Zafra
Analizando imágenes aéreas con Google maps, se observa una forma pentagonal “más afilada” que la presente en la puerta del Cadí. Se caracterizan por definir un triángulo equilátero o isósceles en sus tres lados de cabecera. La forma afilada está en la dirección de acceso, lo cual dificultaba un posible ataque, quedando los ángulos rectos en la parte trasera y los lados laterales junto a un inaccesible acantilado.
Por último, destacamos que la diferencia entre un pentágono con forma afilada, con un ángulo de 60º en la punta como el visto en los castillos anteriores, y uno con un ángulo de 120º, como el empleado en la estructura del puente del Cadí, es clara. El primero tiene un mejor uso para la zona interior del recinto, mientras que para el segundo, el tener el extremo con un ángulo de 120º le ofrece mayor estabilidad a la vez que permite la construcción de la anteriormente descrita escalera interior.
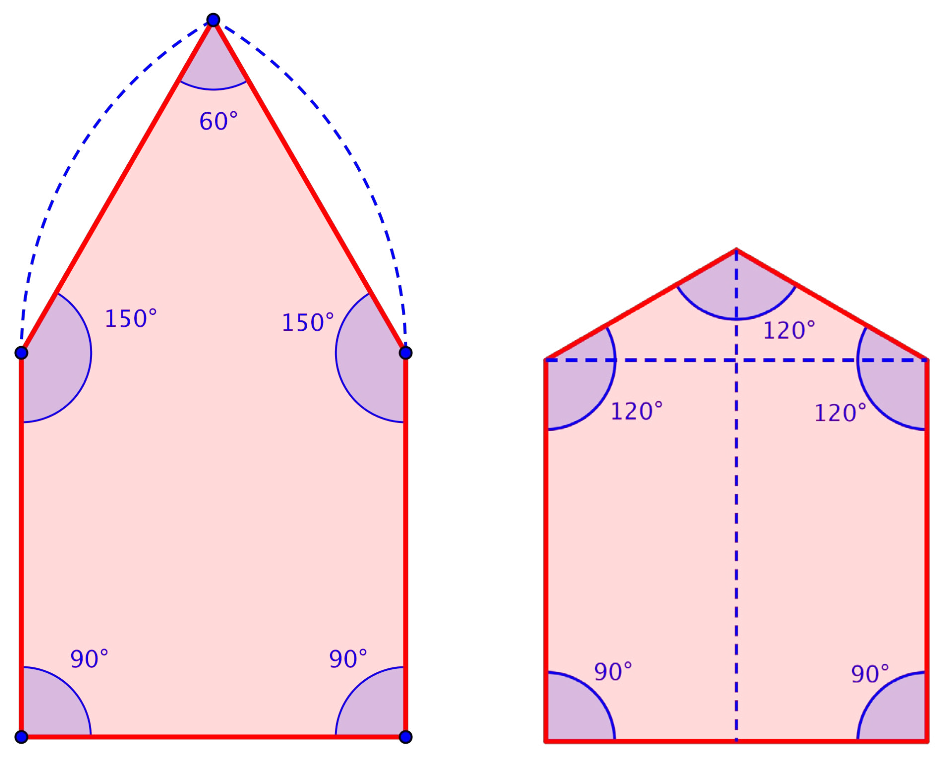
Representación de pentágonos con Geogebra.
Más sobre paseos matemáticos
El Palacio El Baldi de Marrakech (Bab el Mellah, 40000) acoge hasta el 10 de junio la exposición ‘Paseo Matemático al-Ándalus’ de la Fundación Descubre / Consejería de Universidad, Investigación e Innovación de la Junta de Andalucía, una muestra que llega de la mano del Instituto Cervantes en Marrakech.
La Galería Cervantes de Tánger (C/ Bélgica, 9) acoge hasta el 29 de marzo la exposición ‘Paseo Matemático al-Ándalus’ de la Fundación Descubre / Consejería de Universidad, Investigación e Innovación de la Junta de Andalucía, una muestra que llega de la mano del Instituto Cervantes en Tánger.
Durante doce días, y con la financiación de la Embajada de España en Mauritania, Álvaro Martínez Sevilla, director científico del proyecto Paseos Matemáticos, en colaboración con el profesor del Departamento de Lenguaje y Sistemas Informáticos de la Universidad de Granada Sergio Alonso, han recorrido las principales localidades que forman esta ruta para recabar información que les permita realizar un estudio matemático geométrico de la arquitectura y decoración local. Con todo el material recopilado, elaborarán la nueva exposición ‘Paseos Matemáticos Al Ándalus y la ruta de las caravanas’ que se inaugurará en 2025 en la capital mauritana y recorrerá también varias ciudades andaluzas.




