El instante preciso de un frágil equilibrio

Seguimos frente al Ayuntamiento de Granada, cautivados por el extraño encanto con el que observamos la escultura sobre la fachada El instante preciso. Ya en la anterior entrada de este blog caracterizamos los contrastes presentes en la obra de Pérez Villalta en los que se basa esta escultura, siendo éste el elemento predominante en todo el conjunto artístico.

Dibujo de Pérez Villalta

Gracias a la conjunción del bronce y el dorado en la escultura, la estabilidad y a la vez el precario equilibrio que presenta el caballo, la extraña posición de las esferas, la venda en los ojos o la inusual postura del jinete, la obra permite un sinfín de interpretaciones.

Pero la principal referencia parte de la definición que da el propio autor de esta obra, estableciendo que es “un momento de felicidad plena”. El jinete está ante la dorada y redonda perfección de la felicidad, pero es solo un instante, un momento que puede acabar al instante bajo la rotura del precario equilibrio sobre el que se mantiene el caballo.

Además, este desequilibrio se acentúa con el acusado contraste dado por la desproporción de tamaño entre el jinete y el caballo, así como la inusual postura del caballero. También llama la atención como se marcan simultáneamente los músculos en las piernas y glúteos del jinete y también en el caballo. Esta mirada global es lo que ofrece una extraña sensación de desequilibrio. Es más, si atendemos a la posición alta y adelantada de la esfera que sostiene el jinete con su brazo, parece que el conjunto formado por caballo y jinete están en el preciso instante en el que comienza su caída. Una caída sutil que se manifiesta a partir de las condiciones que mantenían el equilibrio.

Para entender mejor esta idea, podemos analizar el centro de gravedad del conjunto de esferas doradas, ya que son las que determinan el supuesto equilibrio inicial y suponiendo que el conjunto formado por el jinete y el caballo está equilibrado.

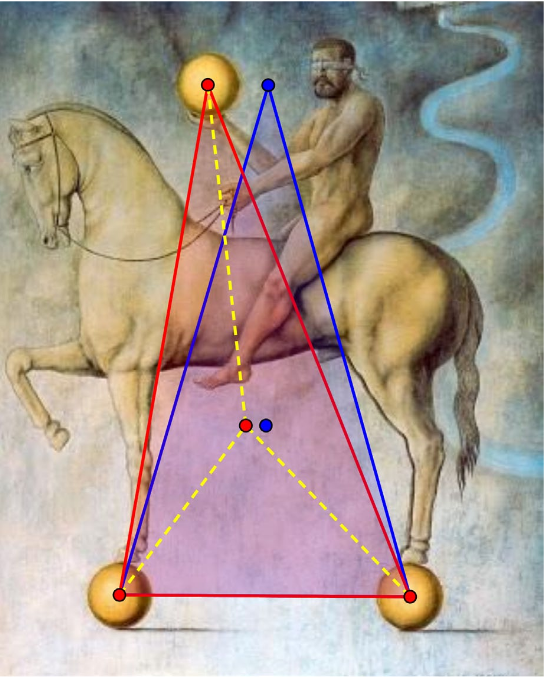
Centro de gravedad en el dibujo

Al ser un dibujo plano, tomamos el centro de gravedad de cada esfera en su centro. Por lo tanto, el centro de gravedad de las tres esferas corresponde con el punto rojo en el que confluyen las tres líneas discontinuas amarillas. Este punto coincide con el baricentro del triángulo, el punto donde se cortan las tres medianas (segmento que une un vértice con el punto medio del lado opuesto).

Una posible situación de equilibrio se correspondería con el triángulo de color azul, el cual se ha trazado para tener un triángulo isósceles a partir de las dos esferas inferiores y considerando la misma altura que la esfera superior para el tercer vértice. El punto en tono azul representa el centro de gravedad de esta posible situación. La diferencia entres ambos puntos es lo que representa la inevitable caída y desplome de este frágil equilibrio.

En cambio, no tenemos la misma sensación si observamos la escultura de Ramiro Mejías sobre la fachada del Ayuntamiento. Esta interpretación parece más realista, ya que la pata delantera del caballo no se equilibra con la pierna del jinete, la cola ondea al viento y hay proporción entre el tamaño del jinete y el del caballo.

Además, dentro de la extraña posición del caballo en equilibrio sobre tres esferas, la escultura transmite mayor sensación de estabilidad. Esto podemos comprobarlo calculando el centro de gravedad del tetraedro irregular (en color rojo) formado a partir de los centros de las cuatro esferas para compararlo con el de la anterior representación.

Centro de gravedad en la escultura

Para el cálculo del centro de gravedad de este tetraedro debemos de calcular el isobaricentro, es decir, el centro de gravedad de cada una de las caras (puntos en color amarillo). Esto se consigue de la misma forma que el cálculo anterior del punto donde se cortan las 3 medianas de cada cara (en color marrón discontinuo y marrón punteado). Después, se toman los segmentos que unen cada isobaricentro de una cara con el vértice opuesto (en color azul continuo). El punto donde se cortan estos 4 segmentos es el centro de gravedad del tetraedro (señalado por un punto de color rojo).

Como conclusión, el centro de gravedad obtenido para la escultura de Ramiro Mejías está más bajo que en el dibujo de Pérez Villanta, lo que conlleva una posición más estable a pesar del aspecto más dinámico que presenta la escultura en comparación con el dibujo.