Seguimos frente a la reja de la calle Oficios, una compleja construcción de superposición de arcos góticos de hierro perfectamente entrelazados. En la anterior entrada destacamos la construcción del arco conopial y de los arcos de medio punto, así que vamos a continuar con el resto de elementos que hemos identificado en este conjunto.

En la misma zona superior de la reja, se observan los arcos trebolados. Este tipo de arcos se construyen a partir de un modelo como el siguiente: se divide la línea de arranques en 4 partes iguales, de manera que el primer y tercer punto que lo dividen, C₁ y C₂, serán los centros de los lóbulos de abajo para que el radio de cada uno sea una cuarta parte del segmento AB. El centro de tercer lóbulo se corresponde con el tercer vértice de un triángulo rectángulo cuya hipotenusa es el segmento C₁C₂.

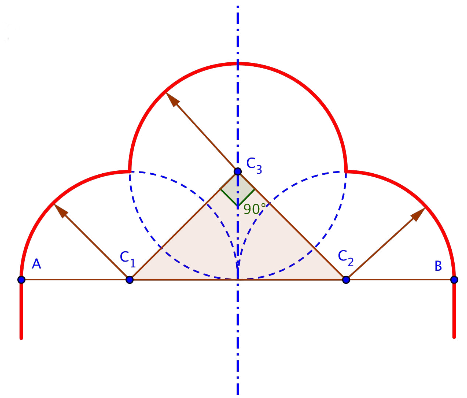
Construcción arcos trebolados.

 Pero la reja de la calle Oficios no guarda esta construcción de manera exacta, ya que el triángulo necesario para definir el centro del lóbulo superior no es rectángulo, sino que tiene unos ángulos de 40º, 40º y 100º. Realizando nuevamente una construcción dinámica con Geogebra, es posible hacer una representación como la que se muestra en la siguiente figura y en la que el punto C₂ sigue marcando una cuarta parte del segmento AB. El conjunto queda rematado con un arco con centro en el punto C₄ que envuelve a los tres lóbulos, el cual se puede obtener como intersección de las dos mediatrices de los lados iguales del triángulo isósceles.

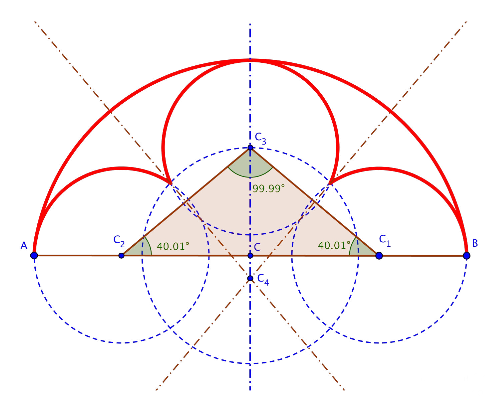
Utilizando esta misma construcción, se puede continuar para completar la construcción de las circunferencias con tetralóbulos inscritos en ellas, que reposan sobre el arco semielíptico y que contienen las iniciales Y y F.

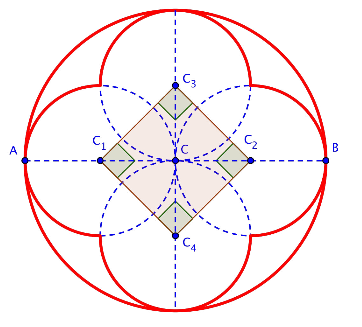
Circunferencia con tetralóbulos.

Por último, queda analizar la construcción del arco descrito por una curva elíptica que queda bajo del dintel del arco conopial. Éste se construye con el popular método del jardinero, partiendo de los dos focos de la elipse, E y F, tomando la intersección de la línea de arranques con la circunferencia de radio la semiluz y centro el punto D del arco buscado.

Así, tomando los focos es fácil trazar una elipse con el software Geogebra. El método del jardinero consiste en tomar una cuerda flexible de longitud la luz del arco apoyada de forma fija en los focos, de manera que la semielipse quedaría marcada al fijar un lápiz al posible movimiento de esta cuerda. De este modo se obtiene el lugar geométrico de los puntos del plano cuya suma de distancias a otros dos fijos, llamados focos, se mantiene constante.

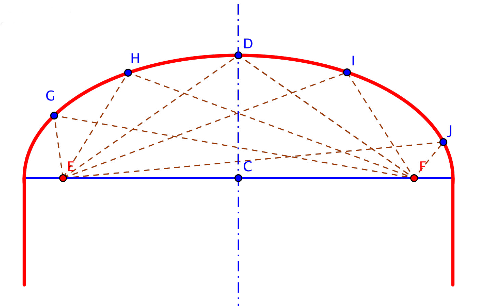
Construcción del arco semielíptico.

Con esto completamos el diseño desde nuestra perspectiva matemática de la reja de la calle Oficios. Una construcción en la que se superponen varias estructuras de arcos y que a pesar de su complejidad, presenta mínimas diferencias con el modelo teórico. Una característica que hace de este trabajo artesano una obra de arte digna de admirar y que no puede faltar en un paseo por la ciudad de Granada.

Un modelo completo trazado con Geogebra quedaría como se muestra en la siguiente imagen:

Construcción completa con Geogebra.