Según el diccionario de la Real Academia Española, un arco conopial es un tipo de arco muy rebajado y con una escotadura en el centro de la clave, que lo hace semejante a un pabellón o cortinaje.

No siempre nos encontramos con la característica de que sea un arco muy rebajado, pero lo que si podemos observar siempre es su escotadura en el centro de la clave con un vértice hacia arriba.

Esto hace que sea similar a la llave mecanográfica con la escotadura hacia arriba ( { ).

Este tipo de arco está muy presente en la arquitectura del gótico tardío, formado con un total de cuatro centros que definen dos semiarcos, cada uno de los cuales tiene un tramo convexo y otro cóncavo.

La construcción matemática de un arco conopial es fácil de realizar con el software Geogebra siguiendo los pasos que se detallan a continuación:

1. Trazar un cuadrado, de manera que cada vértice será el centro de una circunferencia cuyo radio es igual a la mitad del lado del cuadrado. Se puede dejar el trazado y el relleno del cuadrado con poco una tonalidad débil.

2. Trazar las cuatro circunferencias y dejarlas en líneas punteadas para diferenciarlas en el conjunto de la construcción.

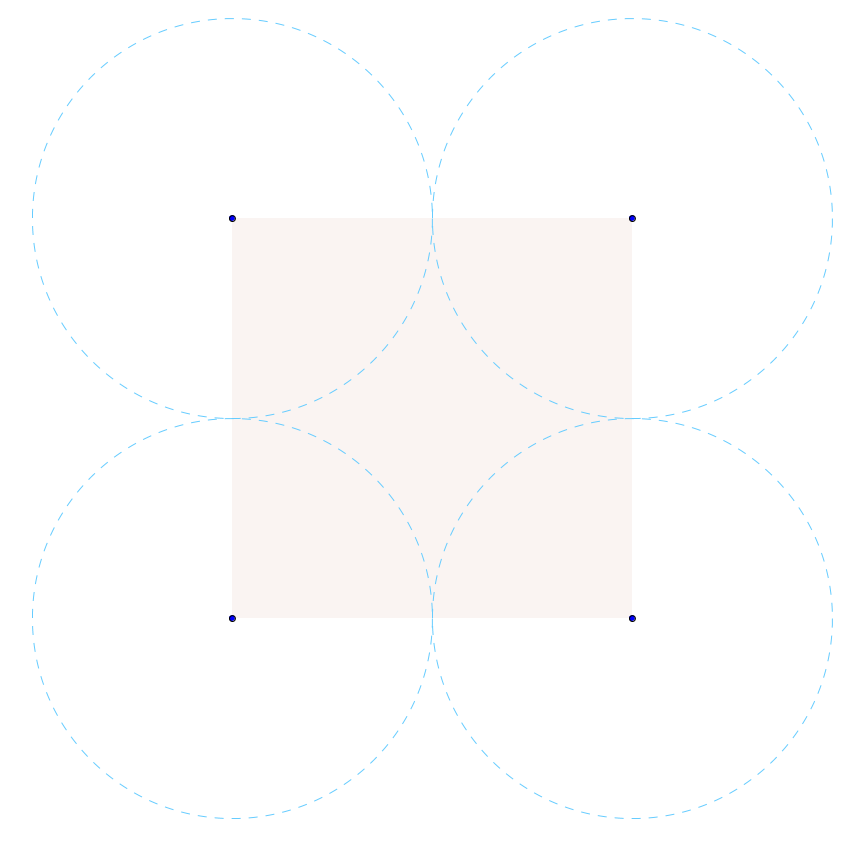
Construcción arco conopial con Geogebra 1.

3. Marcar los puntos de tangencia de las dos circunferencias inferiores con las dos superiores, así como el de las dos superiores entre sí. Marcar igualmente los puntos de las circunferencias inferiores que serán los puntos más bajos del arco.

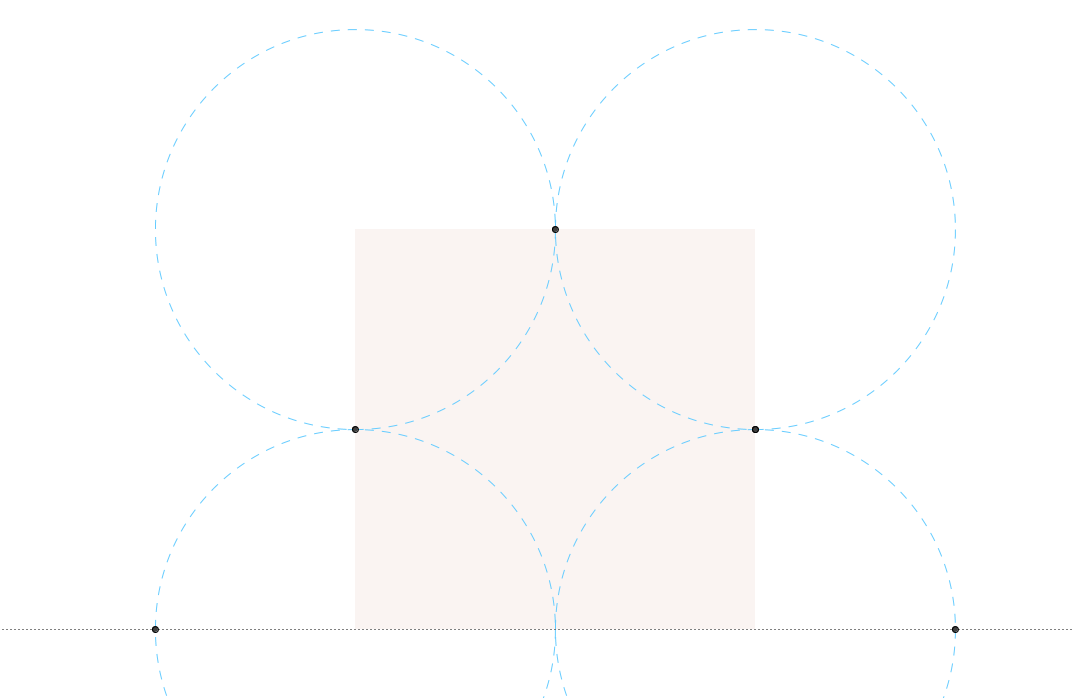
Construcción arco conopial con Geogebra 2.

4. Empleando la herramienta Arco de circunferencia, trazar los arcos que parten desde cada uno de los centros pasando por los puntos marcados anteriormente para definir las zonas cóncavas y convexas del arco conopial.

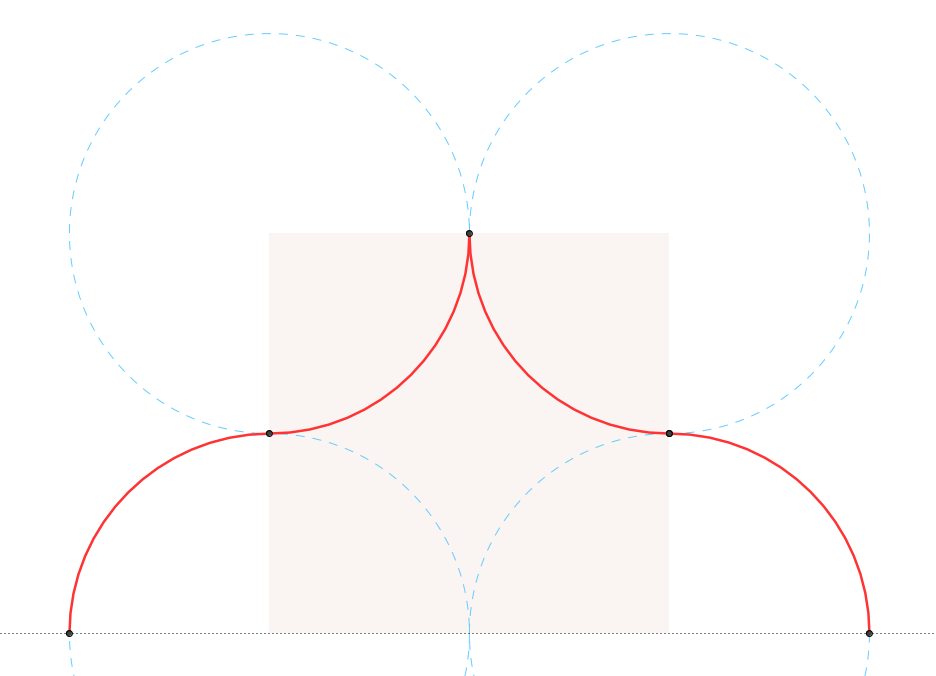
Construcción arco conopial con Geogebra 3.

En nuestro paseo por Granada, no es raro identificar arcos de este tipo. En las tres entradas anteriores se hizo una descripción del conjunto de elementos geométricos que configuran la reja de la calle Oficios, estando éste enmarcado en un destacado arco conopial equilátero.

Reja de la calle Oficios.

Otro importante arco conopial que podemos encontrar en nuestro paseo por Granada es el de la puerta principal del emblemático palacio de Abrantes, situada en la placeta de Tovar.

Puerta del palacio de Abrantes.

Por último, este tipo de arco tan característico del periodo gótico tardío, también conocido como gótico isabelino o estilo Reyes Católicos, lo tenemos presente en la portada interior de la Capilla Real.

Puerta de la Capilla Real.

Como conclusión, no todos los arcos están igualmente rebajados, pero sí que todos mantienen la característica de tener la escotadura en el centro de la clave hacia arriba. Además, todos presentan una misma característica de decoración floral en los semiarcos cóncavos y convexos.