Vesica Piscis en la Casa de los Tiros

La Casa de los Tiros es escenario de numerosos juegos matemáticos, algunos de ellos ya analizados en otro momento de este paseo. Todavía nos queda un asombroso problema: La construcción de la “Vesica Piscis”: una figura muy usada en la iconografía cristiana, y que consiste, básicamente, en hallar dos triángulos equiláteros unidos por su base a partir del lado en común.

Para realizarla necesitamos dos puntos, cuya distancia será el radio de las circunferencias.

En la imagen primera se observa en color naranja que se han tomado en las cabezas de los dos héroes representados en el centro de la fachada (esa línea imaginaria también pasa por encima de los tres polígonos regulares centrales). Esa distancia es igual al lado de los triángulos buscados.

Tomando como centro cada uno de los dos primeros puntos, y como radio la distancia entre éstos, se trazan las dos circunferencias (en azul).

No es una coincidencia que las intersecciones coincidan, arriba, con la cabeza del héroe situado sobre los balcones, y abajo con el punto medio de la base de la puerta de entrada (también en naranja).

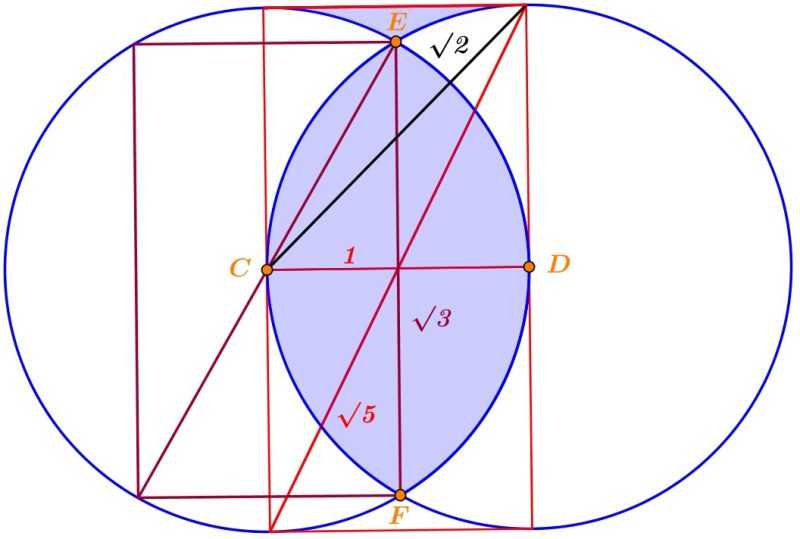
Esta construcción contiene las proporciones de las raíces cuadrada de 2, 3 y 5. Para ello, en la segunda imagen, hemos trazado la figura sobre fondo blanco. Si trazamos los diámetros en la vertical de cada circunferencia, obtenemos un rectángulo de medida 2 (en rojo), cuya diagonal mide la raíz cuadrada de 5. Este rectángulo se divide en dos cuadrados de diagonal raíz cuadrada de 2.

Por último, los puntos superior e inferior de la vesica tienen de longitud la raíz cuadrada de 3 (es decir, la altura de cada triángulo es raíz de 3 partido por 2). La raíz cuadrada de 3 se conoce como constante de Teodoro, en honor a Teodoro de Cirene, filósofo y matemático griego, que desarrolló la teoría de los números irracionales (los que no pueden expresarse como una fracción).