Tres espirales
Los paseos matemáticos por Granada nos permiten hacer un doble recorrido turístico y matemático. Este paseo trata de espirales y arranca en la Casa de los Tiros, donde se encuentra el grabado de Escipión el Africano, retratado con un casco con una espiral geométrica, con radio constante. De ahí, a la plaza del poeta Luis Rosales , donde en una de las caras de la fuente hay una espiral logarítmica, en la que el radio está en función de las potencias de dos. Por último, la Catedral, donde en uno de sus capiteles existe otra espiral, pero en esta ocasión el radio varía según la serie de Fibonacci.
Los paseos matemáticos por Granada nos permiten hacer un doble recorrido turístico y matemático por los monumentos más representativos de la ciudad. También nos da múltiples ejemplos de figuras geométricas cuyas propiedades podemos estudiar usando Geogebra.
Este paseo trata de espirales, y vamos a ver tres ejemplos de espiral geométrica, espiral logarítmica y espiral de Fibonacci. Su clasificación depende de la distancia a la que tomaremos los puntos que pertenecen a la misma recta a la hora de construirla.
Comenzamos por la Casa de los Tiros, el peculiar edificio renacentista del Realejo, cuya fachada ha sido ampliamente estudiada en estos paseos matemáticos. En la primera imagen encontramos una pintura mural situada en el más famoso de sus salones interiores, conocido como “la cuadra dorada”. La figura representa a Escipión el Africano, retratado con un casco con una espiral geométrica.
Estas espirales tienen un radio constante, que no cambia en cada giro (aunque el trazo final diverge para seguir la silueta del casco).
No hay que caminar mucho para llegar a la plaza del poeta Luis Rosales. Sabemos que aunque lleva el nombre del poeta contiene numerosas referencias a las matemáticas.
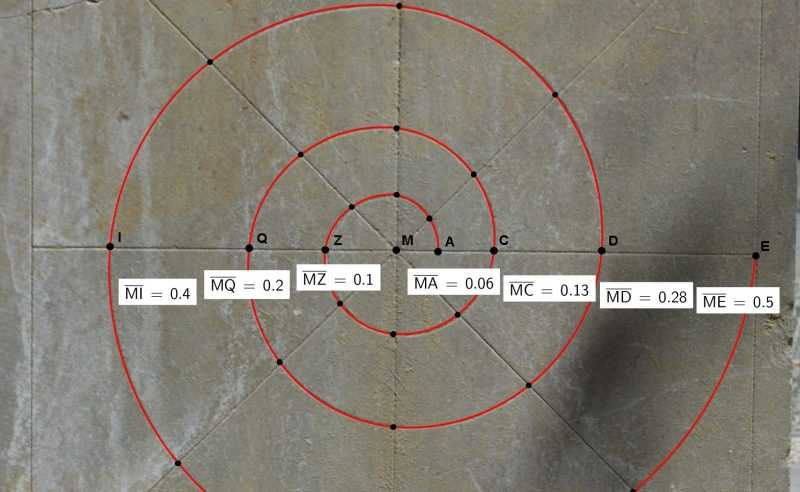
En la segunda imagen aparece una de las caras de la fuente central de la plaza. En ella vemos dibujada una espiral logarítmica. Con Geogebra hemos tomado las distintas distancias entre puntos. Desde el centro a cada uno de ellos va variando, según una función logaritmo de dos. Es algo más fácil de ver en la rama izquierda que en la derecha.
Por último, bajamos un tramo mayor hasta pararnos en la Catedral. Allí vamos a fijarnos en las figuras que adornan uno de sus capiteles. En la tercera imagen vemos cómo hemos sobreimpresionado el análisis de Geogebra al capitel. En primer lugar, en línea discontinua roja se traza el eje de simetría.
Ambas espirales tendrán un estudio similar. Situamos el centro de la espiral en el centro del tocado, y la trazamos rodeando la silueta.
En esta ocasión el radio de la espiral varía de distinta forma que las dos anteriores, pues las distancias siguen la famosa serie de Fibonacci.
Más sobre paseos matemáticos
Las instalaciones del antiguo Consulado francés, ubicadas en el casco antiguo de Trípoli, han acogido la inauguración de la exposición ‘Paseo Matemático al-Ándalus’ de la Fundación Descubre / Consejería de Universidad, Investigación e Innovación de la Juntade Andalucía. La muestra llega de la mano de la Embajada de España en Libia, la Agencia Española de Cooperación Internacional para el Desarrollo (AECID), el Instituto Cervantes y Old Tripoli City Administration Board.
El atún también 'esconde' su lado más matemático y un análisis geométrico de su cuerpo permite diferenciarlos de otros peces. En concreto, se puede saber si un pez es un atún por su cola. Así lo ha analizado en este artículo publicado en el portal web iDescubre por el director científico de Paseos Matemáticos Álvaro Martínez Sevilla. curiosidades que explican por qué este túnido juega un papel destacado en la cultura bereber.
El Instituto Español Lope de Vega de Nador ha acogido la inauguración de la exposición ‘Paseo Matemático Al-Ándalus’ de la Fundación Descubre. La muestra, que inició su andadura por territorio marroquí en Fez en 2023, está itinerando por los Institutos Españoles de Marruecos, gracias al acuerdo con el Instituto Cervantes de Fez.
