Simetrías en la Puerta del Perdón
La Puerta del Perdón, la más esplendorosas de las entradas a la Catedral de Granada, contiene gran cantidad de elementos susceptibles de analizar con las matemáticas en la cabeza, y Geogebra a mano. Una de ellas son las simetrías en las figuras que decoran el intradós del arco.
La Puerta del Perdón es una de la más esplendorosas de las entradas a la Catedral de Granada, aunque está situada en uno de los rincones más estrechos de la manzana, y a veces pasa desapercibida para los turistas. Es una pena, porque contiene gran cantidad de elementos susceptibles de analizar con las matemáticas en la cabeza, y con Geogebra a mano. Atentos al detalle.
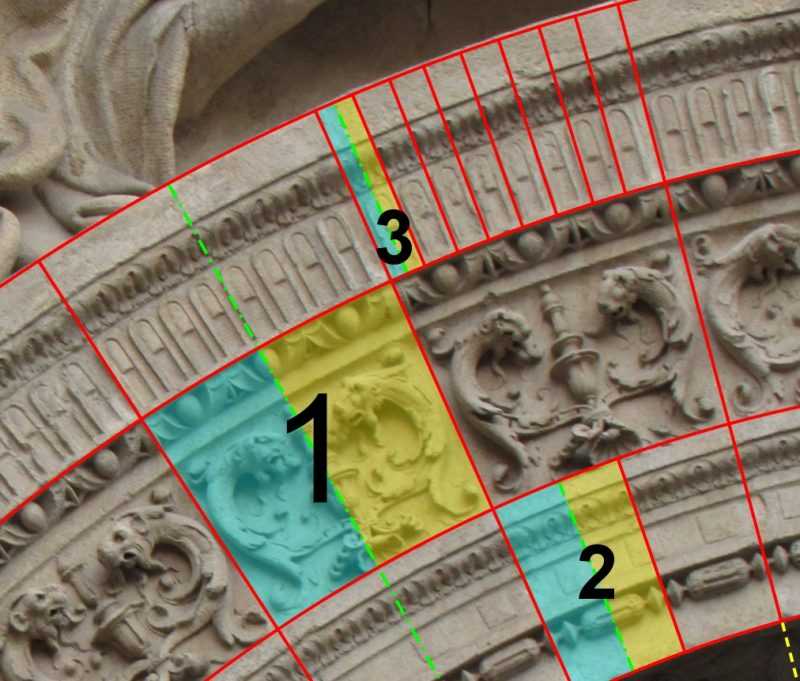
Lo primero que vamos a hacer es analizar las simetrías en las figuras que decoran el intradós del arco, centrándonos en el conjunto que se muestra en la primera imagen. Lo primero que hacemos es trazar, en amarillo y con línea discontinua, el gran eje de simetría axial, que marca cómo se reflejan las figuras al otro lado de este, como el conjunto marcado con un 2. Las figuras marcadas con 1 están, además, nuevamente reflejadas según el eje marcado en verde. Es decir, hay una doble simetría, respecto a los dos ejes, amarillo y verde.
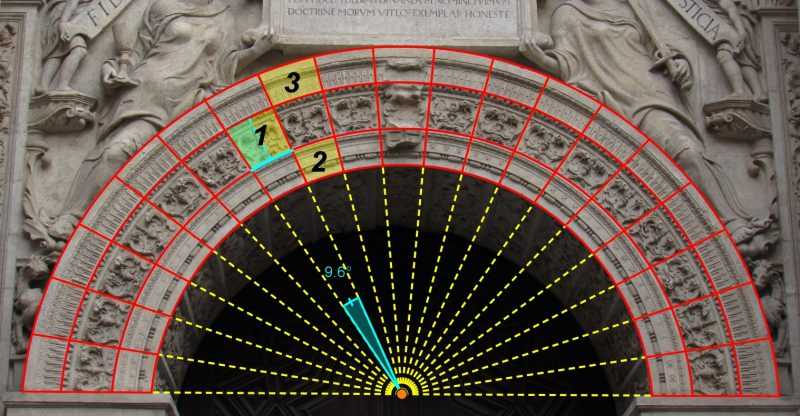
En la segunda imagen se observa en su totalidad el arco principal. Con línea amarilla discontinua se han dibujado los radios que delimitan cada elemento. Salen 19 regiones.
Dividiendo los 180 grados de la semicircunferencia por este número nos sale aproximadamente 9,6 grados de anchura por cada uno (siempre tomando en cuenta las pequeñas desviaciones realizadas por los canteros y los errores de medición). Estos grupos que se van repitiendo mediante el giro de un solo patrón, sin traslación, son conocidos como grupos de Leonardo. Los grupos donde no hay simetría se denominan Cn. Los grupos que analizamos aquí, donde se ha usado simetría, pertenecen al grupo diédrico Dn. Este número n indica las veces que se repite.
Para determinar ese número n, veamos cuántas simetrías se realiza en cada tramo. Hay tres grupos claros, numerados del 1 al 3.
En la tercera imagen se ve con detalle que el primero de los grupos consta de un motivo que se repite, pertenece, pues, al grupo D38 (la circunferencia completa tendría el doble de 19).
La segunda región tiene dos motivos que se repiten con simetría, identificado como D72. Para la tercera región, hay hasta 8 elementos lo que, multiplicando, nos lleva a identificarlo como D304.
Más sobre paseos matemáticos
El atún también 'esconde' su lado más matemático y un análisis geométrico de su cuerpo permite diferenciarlos de otros peces. En concreto, se puede saber si un pez es un atún por su cola. Así lo ha analizado en este artículo publicado en el portal web iDescubre por el director científico de Paseos Matemáticos Álvaro Martínez Sevilla. curiosidades que explican por qué este túnido juega un papel destacado en la cultura bereber.
El Instituto Español Lope de Vega de Nador ha acogido la inauguración de la exposición ‘Paseo Matemático Al-Ándalus’ de la Fundación Descubre. La muestra, que inició su andadura por territorio marroquí en Fez en 2023, está itinerando por los Institutos Españoles de Marruecos, gracias al acuerdo con el Instituto Cervantes de Fez.
La muestra podrá visitarse hasta el 14 de junio en la sala de exposiciones del Castillo.