El lugar geométrico del perdón
La Puerta del Perdón está situada en la angosta calle Cárcel Baja de Granada. La monumentalidad de la fachada queda deslucida porque no es posible tener una visión completa de la misma con una sola mirada. Así que proponemos un nuevo problema matemático: ¿Qué anchura debería tener la calle para apreciarla completamente en el campo de visión del ojo humano? Tomando como referencia que el ángulo de visión debe ser de unos 30 grados, no es difícil plantear el triángulo. Sin embargo, surge una duda, pues el rango de visión depende también de la altura a la que esté el observador.
La Puerta del Perdón es una de las entradas de la Catedral de Granada. Está situada en la calle más estrecha de manzana perímetro, en la angosta calle Cárcel Baja. Por ello, la monumentalidad de la fachada queda deslucida porque no podemos tener una visión completa de las dos plantas que la componen con una sola mirada. Pero eso nos anima a proponer un nuevo problema matemático: ¿Qué anchura debería tener la calle para poder apreciarla completamente de un vistazo, sin movimientos de cabeza? Es decir, ¿Dónde está situado el campo de visión del ojo humano?
Vamos a tomar como referencia que el ángulo de visión debe ser de unos 30 grados, según la bibliografía consultada. Con ello no es difícil plantear el triángulo.
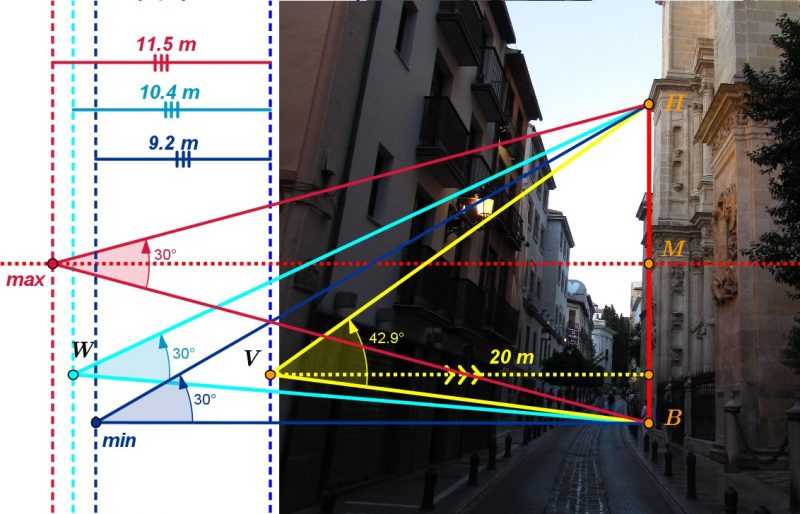
En la primera imagen se muestra el resultado del análisis con Geogebra. Partimos del punto “V” (en amarillo), situado a unos 20 metros de la fachada. También trazamos la altura de la puerta, y los puntos más bajo (B), más alto (H), y el punto medio entre las dos plantas (M).
En este momento nos surge una duda, pues el rango de visión depende también de la altura a la que esté el observador. Por ello vamos a tomar varias alturas, de forma que la solución para una altura máxima (punto rotulado “max”, en rojo) vendrá dada por la altura a la que se sitúa el punto medio entre plantas.
Por el contrario, se considerará mínima (punto rotulado “min”, en azul), a ras del suelo, que es la menor que se podría conseguir de forma física, aunque geométricamente hay otros puntos más bajos con distancias menores.
Por último, tendremos una intermedia (punto rotulado “W”, en celeste), que correspondería a la altura media de una persona adulta de pie. La distancia mínima, según nuestra medida, es de 9.2 metros, mientras que la máxima nos sale 2.3 metros mayor.
Este análisis nos sugiere un nuevo problema: ¿Cómo se distribuyen todos los puntos cuya distancia con la puerta del perdón forma el mismo ángulo de observación?
La solución la encontraremos en la segunda imagen, donde se han conservado los anteriores puntos, y se han trazado dos nuevos, uno por encima de la altura de la puerta, y otro detrás de la misma (ambos en color morado).
El lugar geométrico que encontramos está trazado en rojo, como la silueta que formarían las dos circunferencias secantes que los contiene.
Más sobre paseos matemáticos
El atún también 'esconde' su lado más matemático y un análisis geométrico de su cuerpo permite diferenciarlos de otros peces. En concreto, se puede saber si un pez es un atún por su cola. Así lo ha analizado en este artículo publicado en el portal web iDescubre por el director científico de Paseos Matemáticos Álvaro Martínez Sevilla. curiosidades que explican por qué este túnido juega un papel destacado en la cultura bereber.
El Instituto Español Lope de Vega de Nador ha acogido la inauguración de la exposición ‘Paseo Matemático Al-Ándalus’ de la Fundación Descubre. La muestra, que inició su andadura por territorio marroquí en Fez en 2023, está itinerando por los Institutos Españoles de Marruecos, gracias al acuerdo con el Instituto Cervantes de Fez.
La muestra podrá visitarse hasta el 14 de junio en la sala de exposiciones del Castillo.