El arco conopial
Característico del gótico flamígero, es un tipo de arco de cuatro centros, que se construye a partir de un cuadrado básico de un cuarto de luz. Esta misma medida se toma para el radio de las cuatro circunferencias pequeñas que han de trazarse, y es la mitad del radio de la mayor.
Característico del gótico flamígero, el arco conopial es un tipo de arco de cuatro centros, que se construye a partir de un cuadrado básico de un cuarto de luz (es decir, la cuarta parte de la anchura), y que etiquetamos en naranja como C1, C2, C3 y C4, tal y como puede verse en la primera imagen. Tomando esta medida como radio, se trazan sendas circunferencias tomando como centro cada uno de los vértices del cuadrado, con línea auxiliar.
Estas circunferencias son tangentes dos a dos. Además, las rectas tangentes a estos puntos de corte se intersecan en el centro del cuadrado original. En azul se ha marcado los fragmentos de arco que vamos a coger para la figura final, en la que iremos alternando para conseguir ese efecto de cambio entre cóncavo y convexo.
Si trazamos una circunferencia exterior a las dos circunferencias exteriores, tomando como centro el punto de tangencia entre ambas, y como radio el diámetro de ellas se puede comprobar que su superficie es cuatro veces la cada circunferencia original (debido a que la fórmula de la superficie es pi por el radio al cuadrado, queda multiplicada por cuatro, el cuadrado del doble de la medida original).
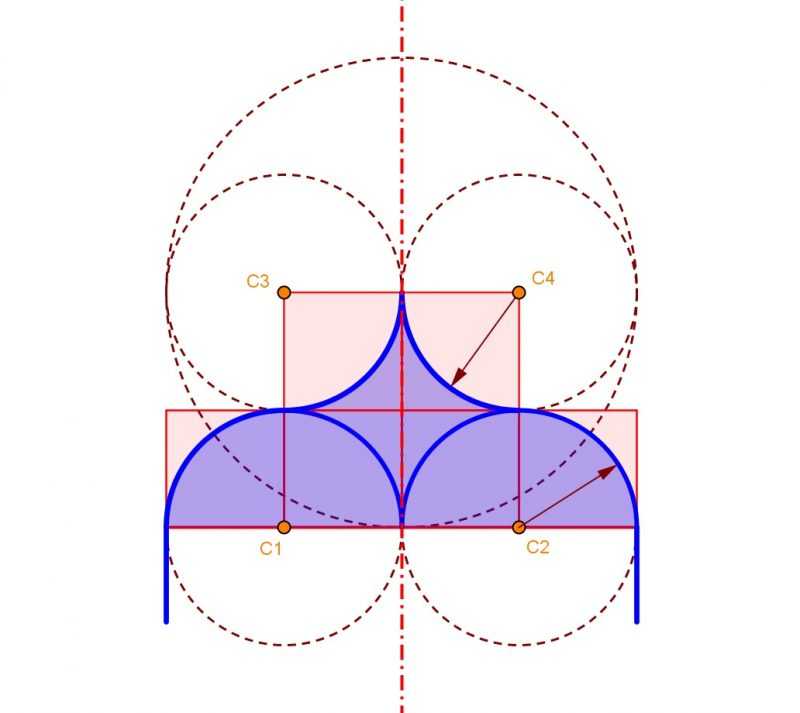
El arco conopial es un tipo de arco de cuatro centros que se construye a partir de un cuadrado básico de un cuarto de luz.
Así, se puede comprobar que la superficie que cubre el arco es 4 veces el cuadrado del radio. Es decir, cuatro cuadrados básicos. A simple vista, basta con darse cuenta de que el fragmento superior se puede construir con las partes que faltan a los lados.
En las imágenes se observa cómo queda la construcción con #Geogebra, a partir de la puerta principal del Palacio de Abrantes, en #Granada. Este análisis realizado en nuestro #paseosmatemáticos revela, además, las imperfecciones que se cometieron en su construcción, quizás porque no fue diseñado con precisión, bien por impericia de los artesanos.
Más sobre paseos matemáticos
El Palacio El Baldi de Marrakech (Bab el Mellah, 40000) acoge hasta el 10 de junio la exposición ‘Paseo Matemático al-Ándalus’ de la Fundación Descubre / Consejería de Universidad, Investigación e Innovación de la Junta de Andalucía, una muestra que llega de la mano del Instituto Cervantes en Marrakech.
La Galería Cervantes de Tánger (C/ Bélgica, 9) acoge hasta el 29 de marzo la exposición ‘Paseo Matemático al-Ándalus’ de la Fundación Descubre / Consejería de Universidad, Investigación e Innovación de la Junta de Andalucía, una muestra que llega de la mano del Instituto Cervantes en Tánger.
Durante doce días, y con la financiación de la Embajada de España en Mauritania, Álvaro Martínez Sevilla, director científico del proyecto Paseos Matemáticos, en colaboración con el profesor del Departamento de Lenguaje y Sistemas Informáticos de la Universidad de Granada Sergio Alonso, han recorrido las principales localidades que forman esta ruta para recabar información que les permita realizar un estudio matemático geométrico de la arquitectura y decoración local. Con todo el material recopilado, elaborarán la nueva exposición ‘Paseos Matemáticos Al Ándalus y la ruta de las caravanas’ que se inaugurará en 2025 en la capital mauritana y recorrerá también varias ciudades andaluzas.





