Un octaedro truncado en tu salón
En el Magreb, los artesanos crean estas curiosas lámparas metálicas con formas muy geométricas, que esconden mucho más de lo que a primera vista parece. Pero, ¿de que objeto matemático se trata?
Es el Octaedro Truncado, uno de los 13 sólidos arquimedianos, poliedros convexos uniformes compuestos de polígonos regulares que se unen en vértices idénticos. Los estudió Arquímedes por primera vez, pero cayeron en el olvido hasta su rescate en el renacimiento. El Octaedro Truncado resulta de seccionar por sus puntas un octaedro (sólido platónico) con lo que se obtienen 8 caras hexagonales y 6 caras cuadradas, todas regulares.
Y tiene una peculiaridad, es uno de los 5 únicos poliedros convexos con caras regulares que son capaces de teselar el espacio tridimensional, es decir de recubrirlo todo sin dejar huecos. Estos son: cubo, prisma triangular, prisma hexagonal (estos 3 derivados de las teselaciones del plano con polígonos regulares), octaedro truncado y el asombrosamente raro y simple girobifastigio (dos prismas triangulares girados y pegados entre si).
Toda una lección de geometría detrás de una simple lámpara domésticas.
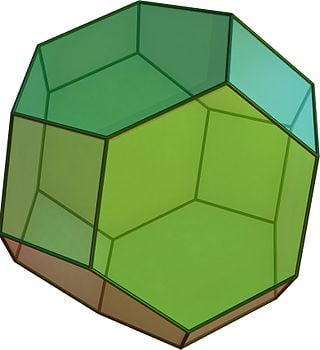
Octaedro truncado
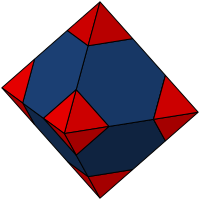
Octaedro regular a partir del cual se realiza la construcción de un octaedro truncado al eliminar las seis pirámides cuadradas.
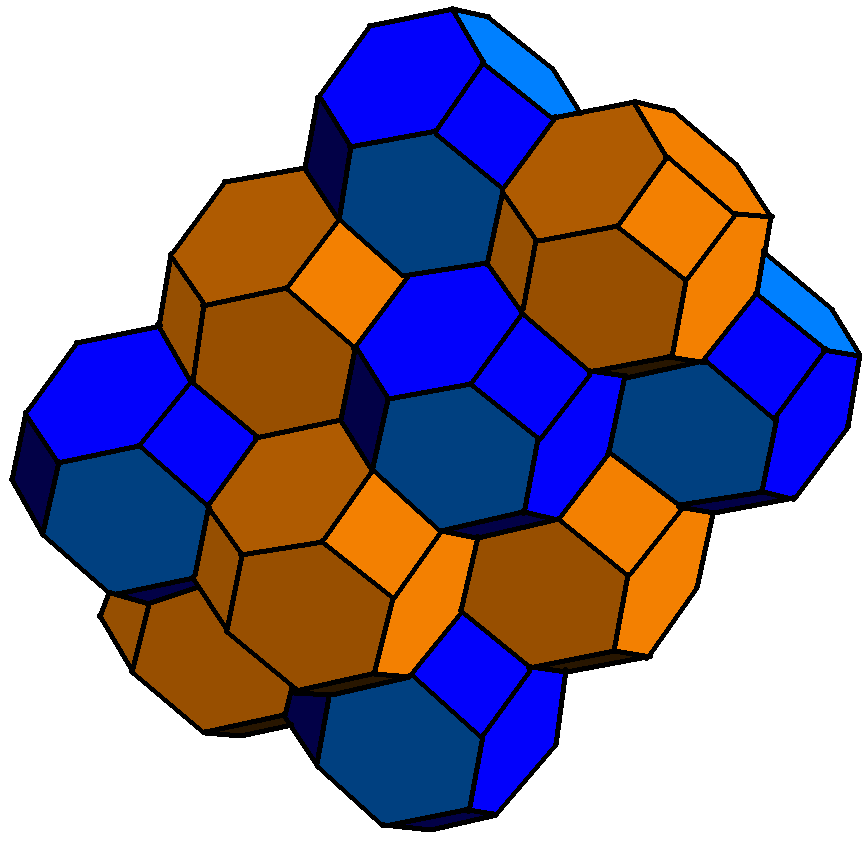
Más sobre paseos matemáticos
Junto con la exposición ‘Paseos Matemáticos Al-Ándalus’, ambas muestras podrán visitarse hasta el 24 de diciembre dentro de las actividades organizadas con motivo de la 14ª edición del Festival de las Ciudades Antiguas, donde España es este año el país invitado de honor.
La muestra permanecerá hasta el 31 de enero en Académie diplomatique internationale de Tunis.
El Espacio Creativo Cultural Santa Clara del Ayuntamiento de Palma del Río acoge la exposición ‘Paseo Matemático al-Ándalus’ de la Fundación Descubre / Consejería de Universidad, Investigación e Innovación de la Junta de Andalucía, una muestra que podrá visitarse hasta el próximo 14 de octubre.
