La recompensa del observador

Siempre hay un premio para el turista observador de estos paseos matemáticos. La recompensa de hoy se encuentra en un lateral de la catedral de Granada, en la conocida como puerta de San Jerónimo; aunque es más conocida por ser lugar donde se sitúan los vendedores ambulantes del tradicional mercado de hierbas.

Es uno de esos detalles que pasan desapercibidos, necesitamos fijarnos bien, pero se puede localizar en la puerta un pentágono de Durero, que es un pentágono regular circunscrito a dos circunferencias concéntricas (que, a su vez, cortan de forma tangencial a los dos rectángulos que enmarcan el conjunto). El polígono regular está decorado con forma de flor, como puede verse en la primera imagen. Esta composición es uno de los pocos adornos con forma explícita de figura geométrica de la Catedral de Granada.

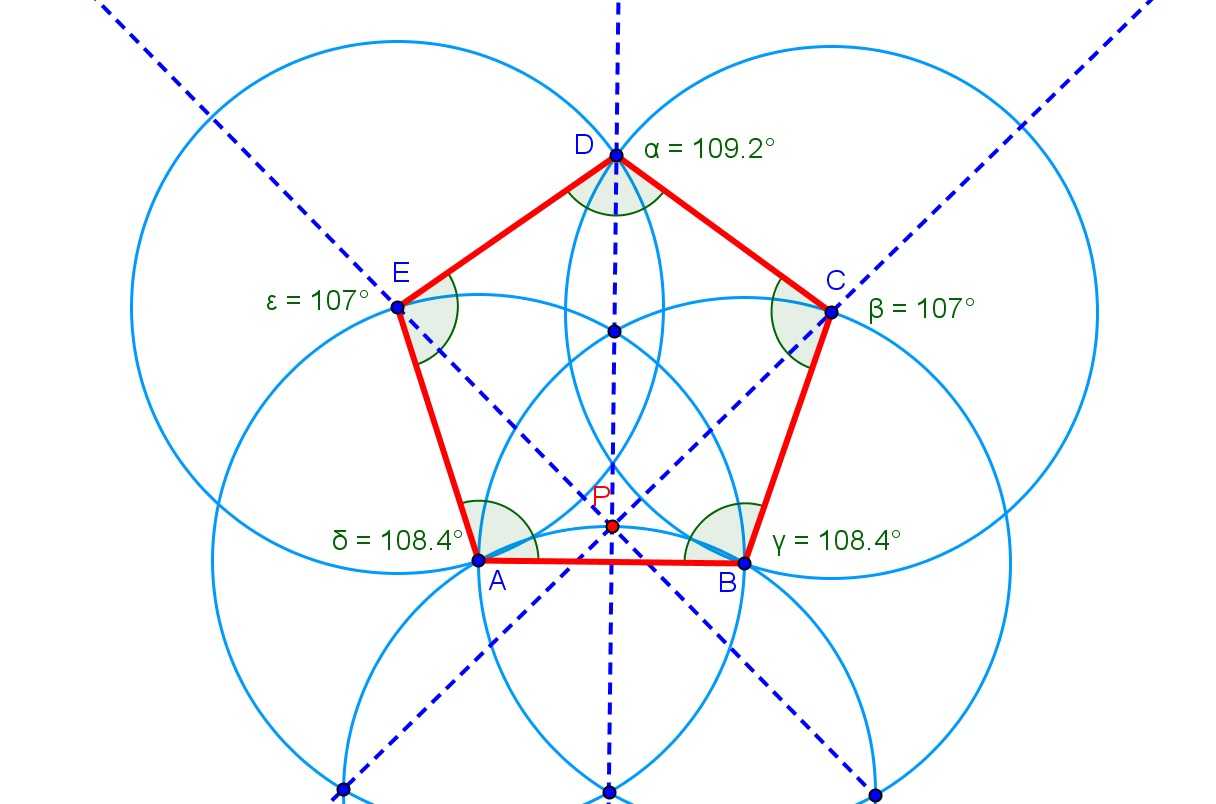
El pentágono regular es una figura muy conocida por los artesanos desde la antigüedad, y se puede construir fácilmente de varias formas (aunque es difícil conseguir que todos los ángulos midan lo mismo). Una de ellas es la conocida como «Pentágono de Durero», cuya construcción se ha replicado con Geogebra en la segunda imagen.

Su construcción se realiza partiendo de la base, desde cuyos vértices se trazan sendas circunferencias con radio igual a esta medida. La intersección inferior de ellas será el centro de otra circunferencia, que cortará a la mediatriz del segmento inicial en un punto P. Uniendo P con cada uno de los puntos de intersección de las dos primeras circunferencias con la tercera, aparecerán los dos vértices siguientes. Desde estos dos trazamos otras dos circunferencias de mismo radio que las anteriores, que coincidirán en el último vértice que necesitamos.

Como característica principal, no cumple que todos los ángulos formen 108º de forma exacta, sino que hay un pequeño error de aproximadamente 1º como máximo.