Dos proporciones en una misma fachada
El Palacio del Duque de Abrantes se encuentra en la placeta de Tovar, en pleno centro histórico. Es un claro ejemplo de arquitectura señorial granadina posterior a 1492. Su bella fachada conserva una puerta principal que ha sobrevivido a las reformas, y luce tal y como fue diseñada, lo que nos va a dar juego para hablar de proporciones. En concreto en esta puerta están reflejadas dos de las más importantes proporciones: la proporción áurea en su puerta principal, y la proporción cordobesa, en la portada que la alberga.
Fachada del Palacio del Duque de Abrantes, en la placeta de Tovar (Granada).
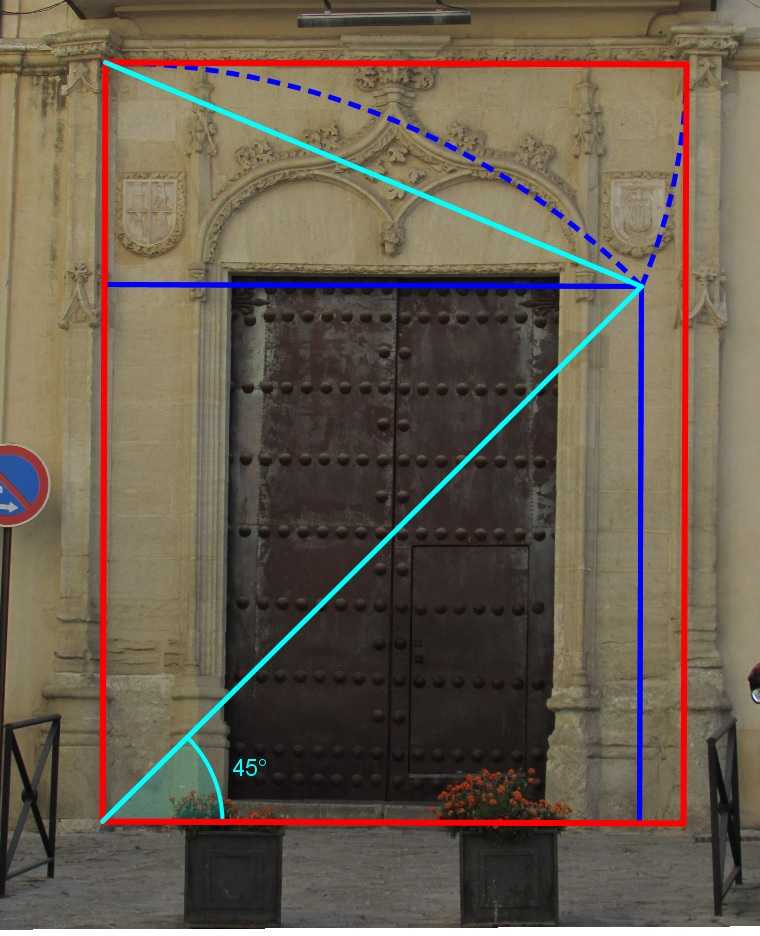
La proporción áurea se construye a partir del cuadrado que tiene como base la longitud horizontal (en nuestro caso, el ancho de la puerta, o luz). Definimos como la unidad a la mitad de esta medida.
Una vez formado el cuadrado, unimos la mitad de una de las alturas (es decir, un punto elevado “una unidad”), con el vértice opuesto; Puede comprobarse que, si un lado tiene una unidad de longitud, y el otro lado tiene dos unidades, la hipotenusa del triángulo que se forma tiene entonces, gracias al teorema de Pitágoras, longitud raíz de 5.
Esta medida debe “abatirse” sobre la altura (trazar un arco con ese radio, que conecte con el segmento. Este trazo está marcado con línea amarilla discontinua). De la división entre los dos lados del rectángulo se obtiene el número áureo phi (o número de oro), que aproximadamente vale 1,618.
La construcción de la proporción cordobesa es un poco más compleja. Su razón es uno a la raíz cuadrada de dos menos raíz de dos. Su cálculo, aproximado, es de 1,306. En geometría se define como la razón entre el radio de una circunferencia y el lado del octógono inscrito en ella.
El rectángulo que vamos a analizar va a comprender las pilastras adosadas a la pared, el borde de la cornisa y el suelo. En primer lugar, se hace la bisectriz (45 grados) del ángulo recto (cuadrado en azul). Tomaremos como radio de la circunferencia el mayor de los lados (marcado en color turquesa). El otro lado se halla buscando el punto de intersección de la bisectriz y la circunferencia. Este lado, trazado en color turquesa, coincide con la medida del lado del octógono anteriormente citado.
Más sobre paseos matemáticos
Las instalaciones del antiguo Consulado francés, ubicadas en el casco antiguo de Trípoli, han acogido la inauguración de la exposición ‘Paseo Matemático al-Ándalus’ de la Fundación Descubre / Consejería de Universidad, Investigación e Innovación de la Juntade Andalucía. La muestra llega de la mano de la Embajada de España en Libia, la Agencia Española de Cooperación Internacional para el Desarrollo (AECID), el Instituto Cervantes y Old Tripoli City Administration Board.
El atún también 'esconde' su lado más matemático y un análisis geométrico de su cuerpo permite diferenciarlos de otros peces. En concreto, se puede saber si un pez es un atún por su cola. Así lo ha analizado en este artículo publicado en el portal web iDescubre por el director científico de Paseos Matemáticos Álvaro Martínez Sevilla. curiosidades que explican por qué este túnido juega un papel destacado en la cultura bereber.
El Instituto Español Lope de Vega de Nador ha acogido la inauguración de la exposición ‘Paseo Matemático Al-Ándalus’ de la Fundación Descubre. La muestra, que inició su andadura por territorio marroquí en Fez en 2023, está itinerando por los Institutos Españoles de Marruecos, gracias al acuerdo con el Instituto Cervantes de Fez.
